Electron Diffraction¶

Background¶

In 1923, in his doctoral dissertation, Louis de Broglie proposed that all forms of matter have wave as well as particle properties, just like light. The wavelength, \(\lambda\), of a particle, such as an electron, is related to its momentum, \(p\), by the same relationship as for a photon:

(1)¶\[\lambda = h/p\]

where \(h\) is Planck's constant. The wave properties of electrons are illustrated in this experiment by the interference, which results when they are scattered from successive planes of atoms in a target composed of graphite micro crystals. The spacing between successive planes is obtainable from the interference pattern.

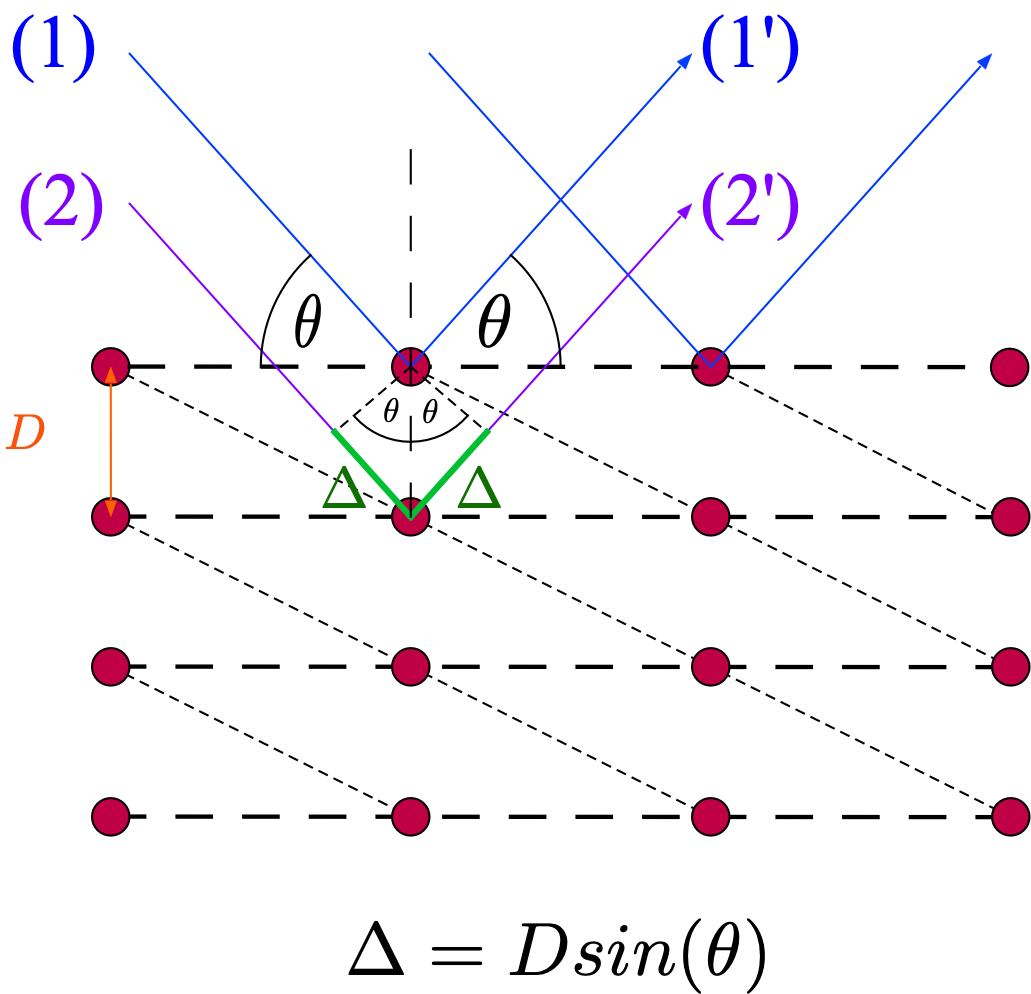
Simple grid with possible atomic planes which reflect incoming X-raus leading to diffraction. Total pathlength difference Delta, between 2 planes.

Figure 1: Reflection of electron waves from atomic planes. Ray 1 and 2 have no path length difference, \(2 \Delta\) is the path length difference between ray 1 from the top plane and ray 3 from the one below. The short-dashed lines show another possible set of atomic planes.

For a single crystal, strong reflection of waves occurs when the Bragg condition is met:

(2)¶\[2d sin(\theta) = n\lambda\ \ (n = 1.,2, ...)\]

In the graphite target, there are very many perfect micro crystals randomly oriented to one another.

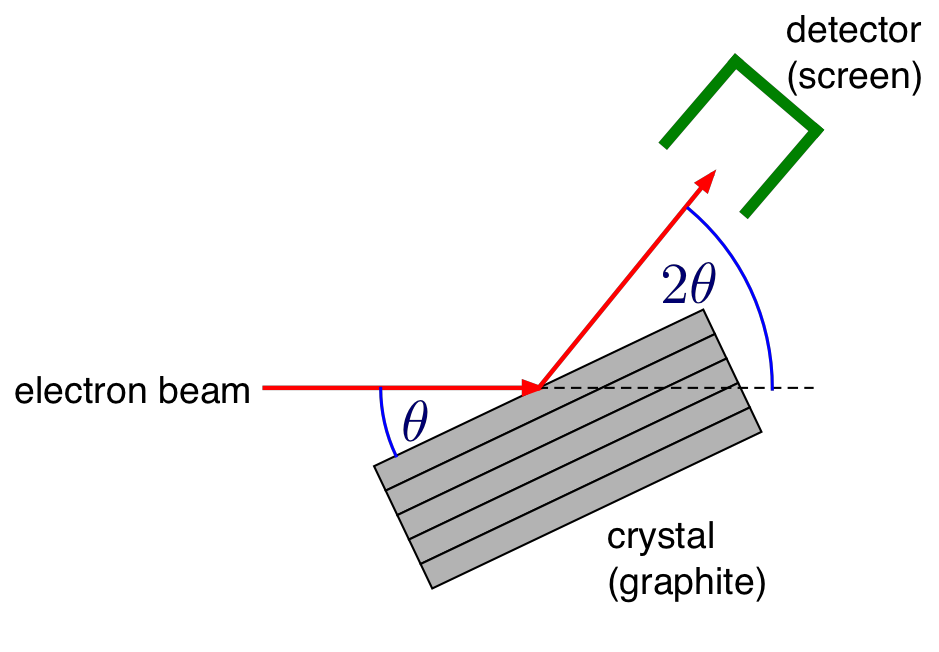
Schematic of electron diffration, incoming electron beam at angle theta with respect to cristal, scattered by 2 theta into detector.

Figure 2: Geometry for diffraction from a single graphite crystal

Therefore the strongly emerging beam will be of a conical shape of half-angle \(2\theta\) as shown in Fig. 3. If this beam falls on a phosphor-coated screen, rings of light will be formed.

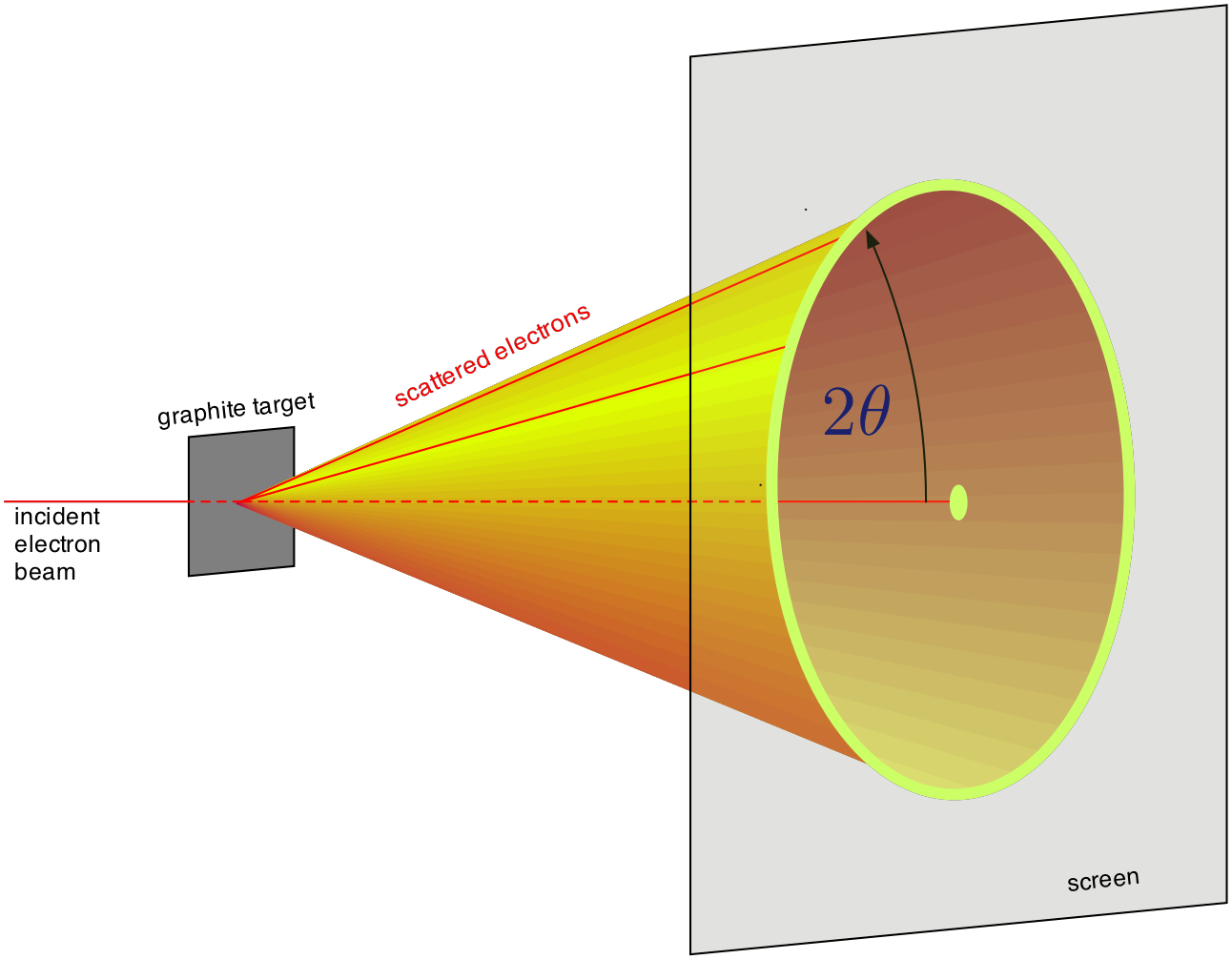
Cone of scattered electrons at 2 theta around incoming beam starting at the target.

Figure 3: Diffraction from a large number of micro crystals

Experimental Setup¶

The apparatus is shown in Fig. 4. Electrons emitted by thermionic emission from a heated filament (4) inside the cathode are accelerated towards the graphite target (9) of the anode by a potential difference, \(V_a\) between the cathode and anode. A focusing electrode (8) is located in front of the target to focus the electron beam in order to provide a sharp interference pattern on the screen (11).

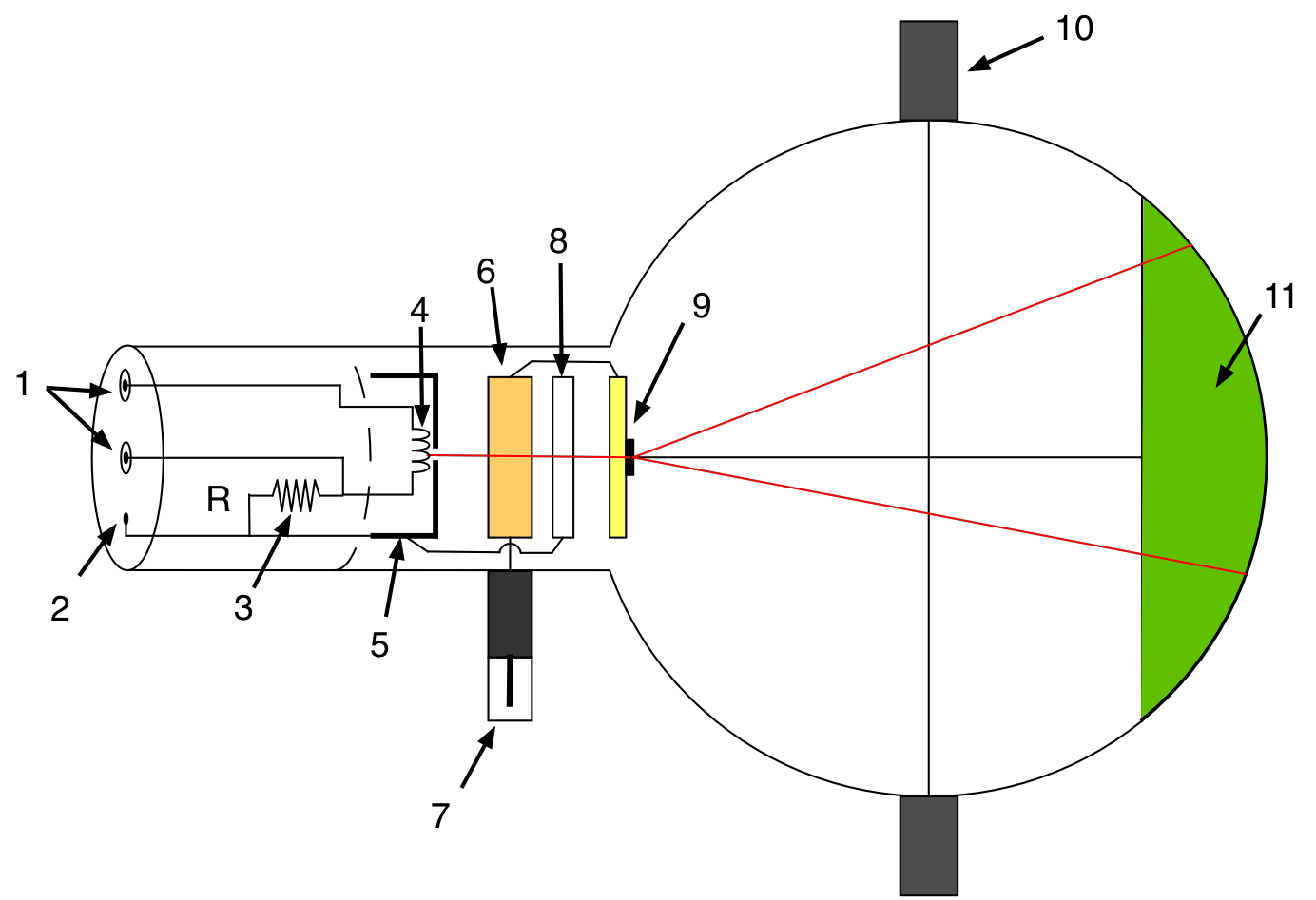
Schematic of electron diffraction tube, with filament, anode, target and screen at the end of the spherical glass type for viewing.

Figure 4: Overview of the electron diffraction tube.(1)4-mm socket for filament heating supply, (2) 2-mm socket for cathode connection, (3) internal resistor, (4) filament. (5) cathode, (6) anode, (7) 4-mm plug for anode connection (HV), (8) focusing electrode, (9) polycrystalline graphite grating, (10) Boss, (11) fluorescent screen.

Their kinetic energy, \(K\), on reaching the target is equal to their loss of potential energy:

(3)¶\[K = \frac{p^2}{2m} = eV_a\]

from equations (1) and (3) one obtains:

(4)¶\[ \begin{align}\begin{aligned}\lambda = \frac{h}{\sqrt{2 m V_a e}}\\\lambda(nm) = 1.228/\sqrt(V_a)\end{aligned}\end{align} \]

Experimental Procedure¶

Connect the power supplies and micro-ammeter to the vacuum tube as shown in Fig. 5

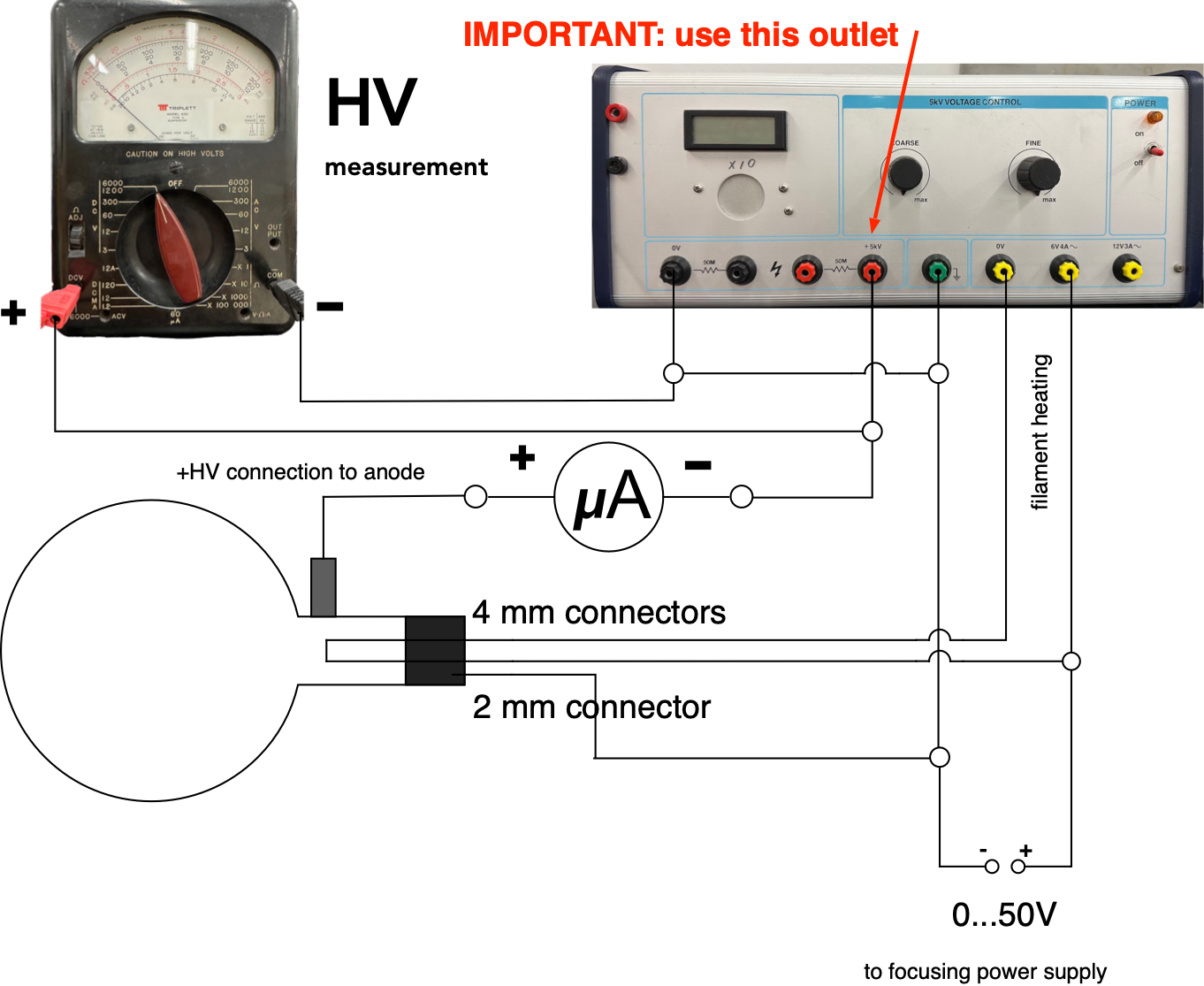
Wiring diagram for electron diffraction tube.

Figure 5: Connecting the electron diffraction tube

HAVE THE CIRCUIT CHECKED BY YOUR INSTRUCTOR BEFORE TURNING ANYTHING ON.

Adjust the voltage controls on the power supplies to zero and then turn them on. Wait a few minutes for the filament to warm up. Set the focusing/intensity voltage to around 30 V and then slowly increase the accelerating voltage to 3 kV. Monitor the electron beam current to ensure that it never exceeds 0.2 mA. A bright central spot and two rings should be observable on the screen. The rings are due to first order (n = 1) diffraction from two different sets of atomic planes having different spacings. Adjust the focusing/intensity voltage until the rings are as sharply defined as possible and then measure their diameters. When adjusting the focus check the current, it should not exceed 0.2 mA. Try to find a setting that produces the best images for the lowest accelerating voltage, where the rings are barely visible, as well as the highest accelerating voltage \(V_a\) (about 5kV) Obtain sets of values of D for different accelerating voltages, \(V_a\), over as wide a range as possible, but not exceeding 5 kV.

You can use a camera to take pictures of the rings and analyze them using the ImageAnalyzer. For help ask an instructor.

Analysis¶

The geometry for the vacuum tube is shown in Fig. 6.

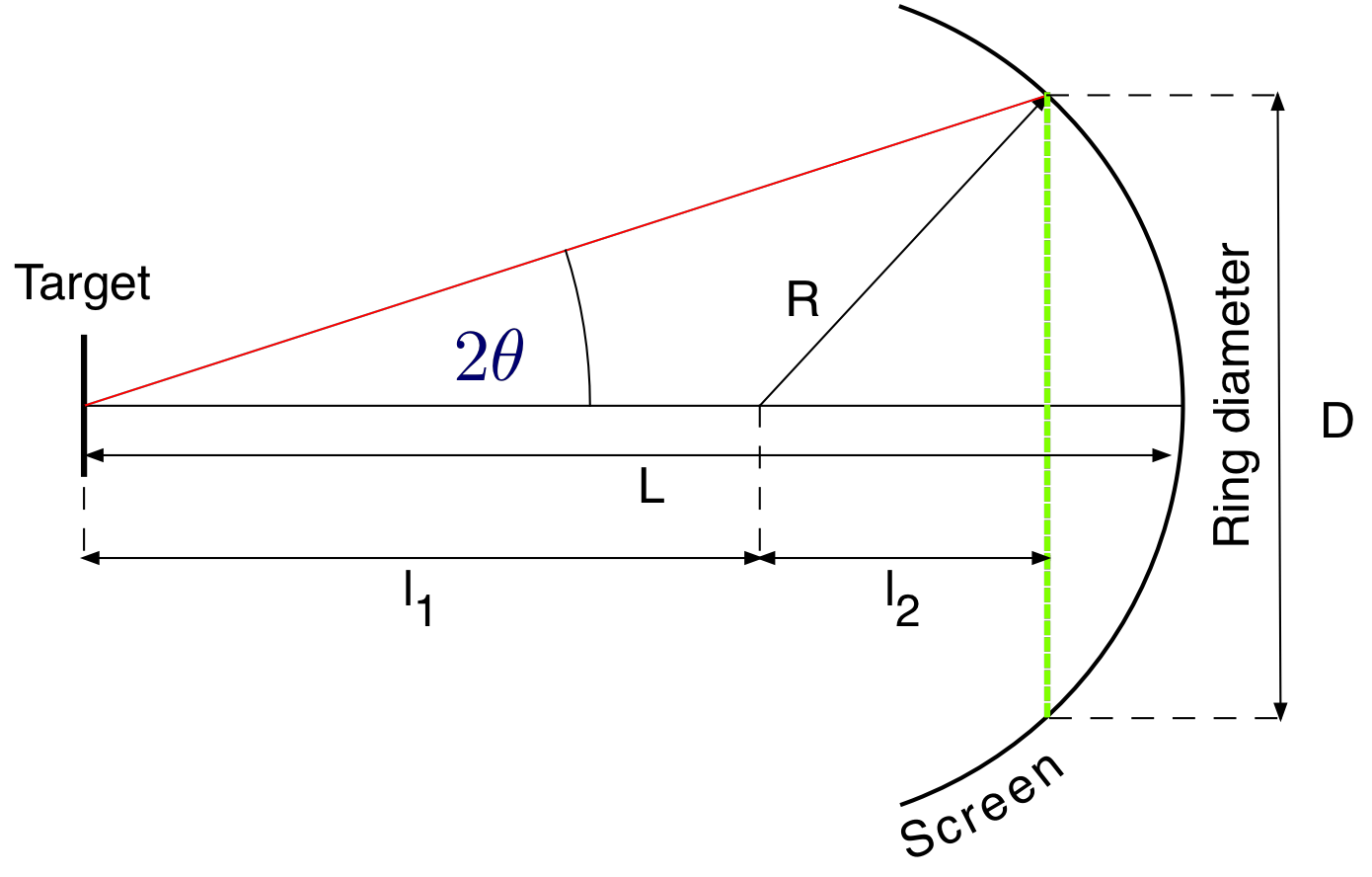
Geometry between target and spherical screen surface and scattering angle.

Figure 6: Vacuum tube geometry

The value of \(\theta\) can be obtained from

(5)¶\[ \begin{align}\begin{aligned}tan(2\theta) = \frac{D/2}{l_1 + l_2}\\l_1 = L - R\\l_2 = \sqrt{R^2 - (D/2)^2}\end{aligned}\end{align} \]

here \(R = 6.25\ cm\) and \(L = 13.7\ cm\). The structure of graphite is shown in Fig. 7. The two possible layers are indicated by dashed lines.

  1. Using these parameters together with your measured voltages and the associated diameters, determine the two different spacings between the planes.

  2. Make a plot of your result as a function of the voltages. Include all error bars. Determine the weighted average values and their uncertainties.

  3. From your measured data determine the distance \(s\) between the carbon atoms and compare your result to the value provided in Fig. 7. Does it agree within error bars ?

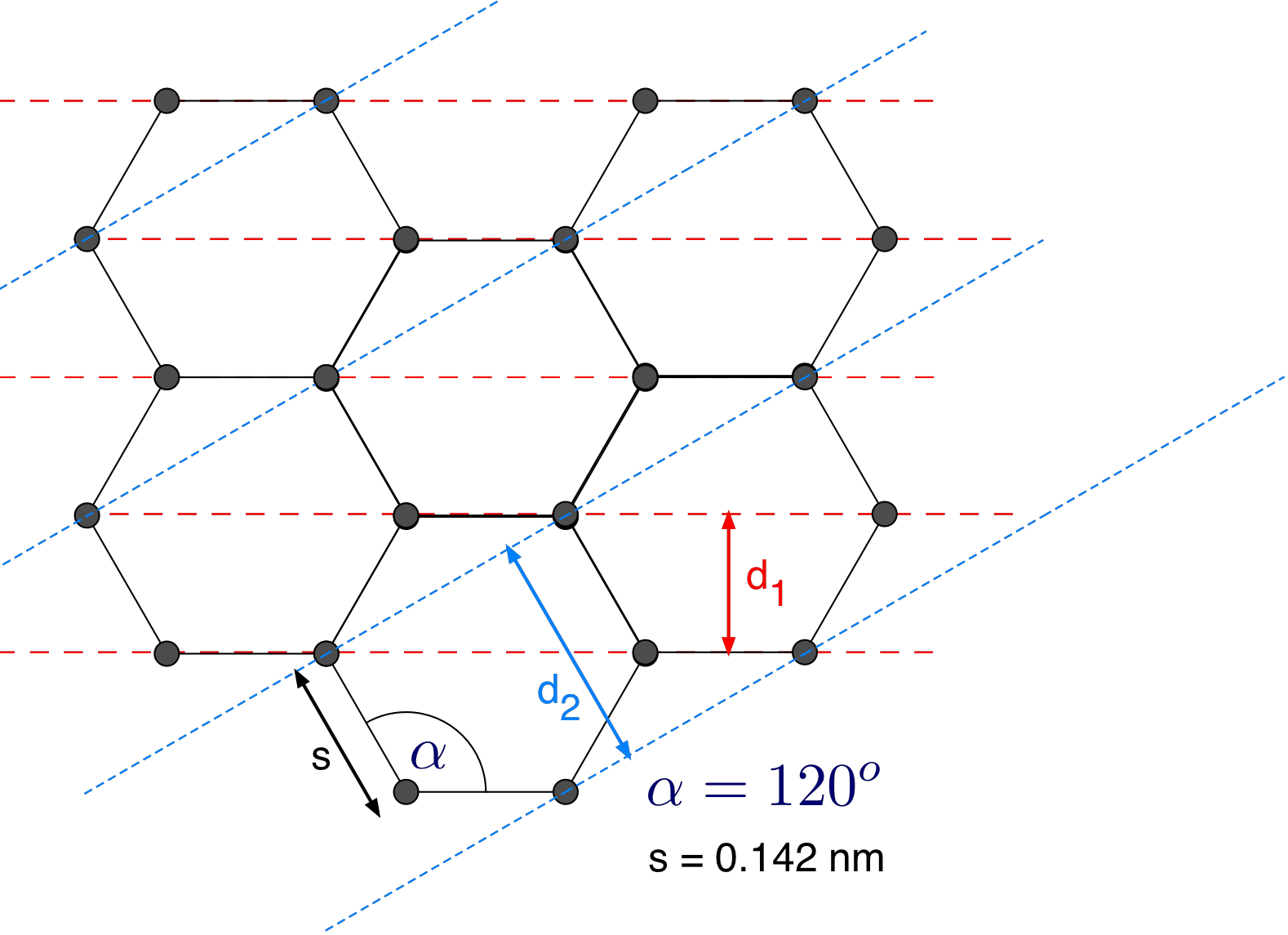
Hexagonal structure of graphite and the two possible planes with distance d1 and d2. s (0.142 nm) is the distance between atoms. Alpha is 120 degrees, the angle between two bonds.

Figure 7: The structure of graphite with Bragg planes.